Let's Learn Recursion in Data Structures with solved questions and easy explanation...
Let's get started.
Q1. on Recursion
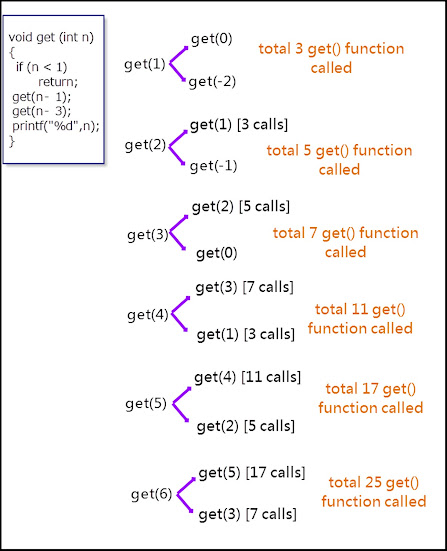
Consider the following recursive C function. If get(6) function is being called in main() then how many times will the get() function be invoked before returning to the main()?void get (int n)
{
if (n < 1) return;
get(n-1);
get(n-3);
printf("%d", n);
}
A. 15
B. 25
C. 35
D. 45
Solution:
B. 25
Explanation:
As per given condition if n < 1 then it return to the main function.
So, Let’s see simple solution in tree form for all values from 1 to 6 for get(6). And find the number of invocation of get() function till condition satisfied.
void count(int n)
{
static int d = 1;
printf("%d ", n);
printf("%d ", d);
d++;
if(n > 1) count(n-1);
printf("%d ", d);
}
int main()
{
count(3);
}
{
static int d = 1;
printf("%d ", n);
printf("%d ", d);
d++;
if(n > 1) count(n-1);
printf("%d ", d);
}
int main()
{
count(3);
}
- GATE-CS-2016 (Set 1)
A. 3 1 2 2 1 3 4 4 4
B. 3 1 2 1 1 1 2 2 2
C. 3 1 2 2 1 3 4
D. 3 1 2 1 1 1 2
Solution:
A. 3 1 2 2 1 3 4 4 4
Explanation:
Explanation:
When count(3) function called:
It will print value of n = 3 and d =1.
And then d++ will change value of d = 2.
Output after count(3) : 3 1
Then count(2) will be called:
It will print value of n = 2 and d = 2.
So 2 2 will be printed and d will become 3. And then d++ will change value of d = 3.
Output after count(2) : 3 1 2 2
Then count(1) will be called:
It will print value of n = 1 and d = 3. And then d++ will change value of d = 4.
Output after count(1) : 3 1 2 2 1 3
After that when condition n>1 becomes false, count(1) will print value of d = 4 and finish its execution. Then count(2) will print value of d = 4. And count(3) will print value of d = 4.
So final Output will be: 3 1 2 2 1 3 4 4 4
int f (int n) {
if (n <= 1) return 1;
else if (n % 2 == 0) return f(n/2);
else return f(3n - 1);
}
Assuming that arbitrarily large integers can be passed as a parameter to the function, consider the following statements.
i. The function f terminates for finitely many different values of n ≥ 1.
ii. The function f terminates for infinitely many different values of n ≥ 1.
iii. The function f does not terminate for finitely many different values of n ≥ 1.
iv. The function f does not terminate for infinitely many different values of n ≥ 1.
Which one of the following options is true of the above?
- Gate IT 2007
A. i and iii
B. i and iv
C. ii and iii
D. ii and iv
Solution: D. ii and iv
It will print value of n = 3 and d =1.
And then d++ will change value of d = 2.
Output after count(3) : 3 1
Then count(2) will be called:
It will print value of n = 2 and d = 2.
So 2 2 will be printed and d will become 3. And then d++ will change value of d = 3.
Output after count(2) : 3 1 2 2
Then count(1) will be called:
It will print value of n = 1 and d = 3. And then d++ will change value of d = 4.
Output after count(1) : 3 1 2 2 1 3
After that when condition n>1 becomes false, count(1) will print value of d = 4 and finish its execution. Then count(2) will print value of d = 4. And count(3) will print value of d = 4.
So final Output will be: 3 1 2 2 1 3 4 4 4
Q3. On Recursion
The function f is defined as follows:int f (int n) {
if (n <= 1) return 1;
else if (n % 2 == 0) return f(n/2);
else return f(3n - 1);
}
Assuming that arbitrarily large integers can be passed as a parameter to the function, consider the following statements.
i. The function f terminates for finitely many different values of n ≥ 1.
ii. The function f terminates for infinitely many different values of n ≥ 1.
iii. The function f does not terminate for finitely many different values of n ≥ 1.
iv. The function f does not terminate for infinitely many different values of n ≥ 1.
Which one of the following options is true of the above?
- Gate IT 2007
A. i and iii
B. i and iv
C. ii and iii
D. ii and iv
Solution: D. ii and iv
Explanation:
The function f is terminated for any value of n which is, power of 2. There are infinite numbers, which are power of 2.
The function f is terminated for any value of n which is, power of 2. There are infinite numbers, which are power of 2.
Therefore,
(ii) The function f terminates for infinitely many different values of n ≥ 1.
In this "infinitely many different values of n>=1" means infinite numbers. So, It is correct.
(i) The function f terminates for finitely many different values of n ≥ 1.
In this "finitely many different values of n>=1" means finite numbers. So, It is incorrect.
(iii) The function f does not terminate for finitely many different values of n ≥ 1.
In this "finitely many different values of n>=1" means finite numbers. So, It is incorrect.
(iv) The function f does not terminate for infinitely many different values of n ≥ 1.
In this "infinitely many different values of n>=1" means infinite numbers. So, It is correct.
Q4. On Recursion
Consider the code fragment written in C below :void f (int n)
{
if (n <=1)
{
printf ("%d", n);
}
else
printf ("%d", n);
}
else
{
f (n/2);
printf ("%d", n%2);
}
}
f (n/2);
printf ("%d", n%2);
}
}
What does f(173) print?
- Gate IT 2008
A. 010110101
B. 010101101
C. 10110101
D. 10101101
Solution: D. 10101101
B. 010101101
C. 10110101
D. 10101101
Solution: D. 10101101
Explanation:
The f(int n) function return binary digit of decimal n number.
Binary number of 172 is 10101101.
Q5. On Recursion
In general, in a recursive and non-recursive implementation of a problem (program) :- UGC NET CS 2015 Dec - II
A. Both time and space complexities are better in recursive than in non-recursive program.
B. Both time and space complexities are better in non-recursive than in recursive program
C. Time complexity is better in recursive version but space complexity is better in non-recursive version of the program.
D. Space complexity is better in recursive version but time complexity is better in non-recursive version of the program.
Solution:
B. Both time and space complexities are better in non-recursive than in recursive program.
Explanation:
In general, in a recursive and non-recursive implementation of a problem (program), Both time and space complexities are better in non-recursive than in recursive program.
Consider the following C-program:
void foo(int n, int sum)
{
int k = 0, j = 0;
if (n = = 0) return;
k = n % 10;
j = n / 10;
sum = sum + k;
foo (j, sum);
printf ("%d,", k);
}
int main ()
{
int a = 2048, sum = 0;
foo (a, sum);
printf ("%d\n", sum);
getchar();
}
What does the above program print?
Q6. On Recursion
Consider the following C-program:void foo(int n, int sum)
{
int k = 0, j = 0;
if (n = = 0) return;
k = n % 10;
j = n / 10;
sum = sum + k;
foo (j, sum);
printf ("%d,", k);
}
int main ()
{
int a = 2048, sum = 0;
foo (a, sum);
printf ("%d\n", sum);
getchar();
}
What does the above program print?
- GATE-CS-2005
A. 8, 4, 0, 2, 14
B. 8, 4, 0, 2, 0
C. 2, 0, 4, 8, 14
D. 2, 0, 4, 8, 0
Solution: D. 2, 0, 4, 8, 0
Explanation:
foo function prints all the digits of a number stored in variable a.
In code, k= n % 10 modulus operator will return the remainder. for n=2048, then k = 2048 %10 will store the value k = 8.
j is integer datatype in foo function. So, after division if the decimal part will be truncated and only the integer part will be stored in j. For j=2048/10, j = 204.8, but decimal part will truncated, so j =204.



0 Comments